|
[Opération bit-à-bit] Retrouver la clé d'une opération XOR
|
|
21-09-2013, 23h19
(Modification du message : 22-09-2013, 21h21 par Kiwazaru.)
Message : #1
|
|
Kiwazaru

Padawan d'un super escargot  Messages : 284 Sujets : 26 Points: 139 Inscription : Mar 2012 |
[Opération bit-à-bit] Retrouver la clé d'une opération XOR
Salut à tous !
Je vais vous parler d'un sujet que vous devez connaître, mais pas en profondeur pour certains. Les opérations bit-à-bit sont des outils qui permettent de traiter une valeur pour la modifier. A la base, c'est surtout utilisé en électronique. Mais on peut aussi les utiliser en cryptographie pour chiffrer une chaîne par exemple. Ici on va parler du XOR. Beaucoup d'entre vous connaissent l'astuce: Plaintext XOR Ciphertext = Key Mais à mon avis, beaucoup le savent sans savoir pourquoi aussi. C'est le but de ce post (ce n'est pas très long). Commençons par le commencement. Qu'est-ce qu'un XOR ? Eh bien c'est un OU Exclusif. Ses propriétés sont les suivantes: 0 XOR 0 == 0 0 XOR 1 == 1 1 XOR 0 == 1 1 XOR 1 == 0 Un XOR prend donc en compte deux valeur sur l'intervalle [0;1] soit VRAI ou FAUX. La valeur de retour vaut VRAI si et seulement si les deux valeurs XORÉ ne sont pas identiques. Pour que la valeur de retour soit 1, il faut alors que les deux valeurs XORÉ soient 0 et 1. Dans le cas contraire, le XOR renvoi FAUX Prenons un exemple: 7 XOR 3 = 4 En binaire: 0111 XOR 0011 = 0100 Nous allons remarquer la puissance de cette propriété. Ici, on a comme plaintext 0111 et comme ciphertext 0100 Un XOR s'effectue bit-à-bit donc nous prenons en premier: 0 ^ 0, les deux valeurs sont identiques, nous avons donc 0 en retour, notre clé étant 0011 le début est vrai. En deuxième valeur nous avons 1 ^ 1 et cela nous renvoi encore 0 nous sommes encore bon sur la clé, nous avons donc le début de la clé qui est 00??. Ensuite nous avons 0 ^ 1 qui nous renvoi 1, la suite de la clé est donc 001?, cela correspond bien. Enfin nous avons 0 ^ 1 encore une fois qui nous renvoi 1, la clé est donc 0011. Cela vient tout simplement du principe du XOR qui nous permet cette exploitation. Avec un AND, OR cela ne marchera pas car les propriétés ne sont pas les mêmes, entre autre pour un AND par exemple, 1 & 0 donne 0 ansi que 0 & 0 donne 0. Nous aurions donc deux valeurs possible et donc un résultat non vérifiable. Le OR a le même système, mais à l'inverse, il donne 1 pour 0 | 1 et 1 pour 1 | 1. Contrairement à ces deux opérations, le XOR est facilement renversable puisqu'il renvois 0 dans deux cas qui sont que les deux valeurs sont identiques. Dans notre ciphertext quand nous voyons 0 nous savons donc que le xor s'est passé avec 1 ^ 1 ou 0 ^ 0. Vu que ce n'est pas si simple que ça à expliquer, je vais utiliser un dernier exemple pour vous faire bien comprendre. Prenons, 5 XOR 6 = 0 On a donc: 0101 XOR 0110 = 0011 Imaginons que l'on nous donne comme énoncé: Nous avons 0101 qui a été XOR par une valeur inconnue, mais nous avons le résultat qui vaut 0011. Trouvez la clé du XOR. On voit que le premier bit du résultat vaut 0 et que le premier bit du plaintext vaut aussi 0. On sait alors que le XOR du premier bit a été 0 ^ 0. On prend le deuxième bit du résultat et du plaintext. On a comme résultat 0 avec un bit 1 xoré par quelque chose. Si ce bit avait été xoré avec 0 alors on aurait eu un résultat de 1 , il a donc été xoré avec un autre 1 pour obtenir 0. Prenons le troisième bit, celui du résultat vaut 1 et celui du plaintext vaut 0. Si nous avons un résultat de 1 alors les deux bits initialement xoré n'étaient pas identiques. Sachant que le bit du plaintext vaut 0, celui de la clé était donc de 1. Notre clé formée vaut donc pour le moment 011? Prenons le dernier bit du résultat qui vaut 1 et celui du plaintext qui vaut 1. Si le résultat vaut 1 et que le bit du plaintext vaut 1, alors ce 1 a été xoré par un 0 pour obtenir 1. Notre clé finale est donc 0110. Un moyen mémotechnique pour certains peut être de se l'imaginer sous forme d'équation, sans changement de signe. ![[Image: 594618tex2png10cgi.png]](http://img15.hostingpics.net/pics/594618tex2png10cgi.png) Une petite suite de XOR simple à faire de tête: 1001 XOR 0110 = ? 1111 XOR 0000 = ? 1000 XOR 0010 = ? 1101 XOR 0010 = ? 0000 XOR 0000 = ? 1111 XOR 1111 = ? 1010 XOR 0101 = ? 1100 XOR 1011 = ? 1000 XOR 1111 = ? 0111 XOR 1001 = ? Une fois que vous aurez bien réussi à faire ces XOR de tête, je vous donne une suite de Plaintext accompagné de leur Résultat. Il faudra retrouver la clé. Plaintext , Ciphertext => Key 1000 , 1101 => ? 0001 , 0000 => ? 1001 , 1110 => ? 0101 , 0100 => ? 0011 , 1011 => ? 0110 , 0010 => ? 0111 , 0000 => ? 1001 , 0001 => ? 0010 , 0101 => ? 1000 , 1011 => ? Essayez de raisonner avec mon système de comparaison résultat/plaintext et de ne pas faire le xor automatiquement ! N'hésitez pas à réagir sur le sujet 
Toucher au Kernel, c'est un peut comme se shooter au LSD, on pense pouvoir tout faire mais ça finit souvent mal.
|
|
|
|
|
22-09-2013, 11h15
(Modification du message : 22-09-2013, 11h19 par InstinctHack.)
Message : #2
|
|
InstinctHack

Posting Freak  Messages : 1,366 Sujets : 184 Points: 299 Inscription : Dec 2011 |
RE: [Opération bit-à-bit] Retrouver la clé d'une opération XOR
Sympa le post
 3 bricoles : Citation :0 XOR 0 == 0Autant mettre la table de vérité en entier ihmo. 0 XOR 0 == 0 0 XOR 1 == 1 1 XOR 0 == 1 1 XOR 1 == 0 Citation :La valeur de retour vaut VRAI si et seulement si les deux valeurs XORÉ ne sont pas identiques.tu peux remplacer "ne sont pas identiques" par "sont identiques" c'est plus simple à lire ihmo. Et dernière proposition : mettre les solutions des xor lisibles uniquement au survol à coté des questions, ça permet à ceux qui ferait l'exercice de pouvoir se corriger ihmo.  Sinon merci pour ce post. 
Citation :un jour en cours de java j'ai attrapé les seins d'une fille mais elle m'a frappé en disant "c'est privé !!" |
|
|
|
|
22-09-2013, 11h34
Message : #3
|
|
supersnail

Éleveur d'ornithorynques        Messages : 1,609 Sujets : 71 Points: 465 Inscription : Jan 2012 |
RE: [Opération bit-à-bit] Retrouver la clé d'une opération XOR
Sinon pour les plus matheux d'entre vous, on peut voir le XOR comme une addition dans le groupe ℤ/2ℤ, où on a la propriété suivante (bon c'est pas trop formel, mais un peu quand-même):
∀ x ∈ ℤ/2ℤ, x + x = 0 (0 étant l'élément neutre), du coup on a: ∀ x,y ∈ ℤ/2ℤ, x + y + x = x + x + y = 0 + y = y  (ℤ/2ℤ est commutatif :þ) (ℤ/2ℤ est commutatif :þ)
Mon blog
Code : push esp ; dec eax ; inc ebp ; and [edi+0x41],al ; dec ebp ; inc ebp"VIM est merveilleux" © supersnail |
|
|
|
|
22-09-2013, 11h55
(Modification du message : 22-09-2013, 12h13 par b0fh.)
Message : #4
|
|
b0fh

Membre actif  Messages : 210 Sujets : 17 Points: 309 Inscription : Jul 2012 |
RE: [Opération bit-à-bit] Retrouver la clé d'une opération XOR
Pour les moins matheux d'entre vous: (ℤ/2ℤ,+,.) correspond à l'arithmétique "classique" sur les entiers, dans lesquels on ne s'inquièrerait pas de la valeur d'un nombre, mais seulement de savoir s'il est pair ou impair.
On remarque que le ⊕ (xor) correspond à l'addition, parce que nombre pair + nombre pair = nombre pair nombre impair + nombre pair = nombre impair nombre pair + nombre impair = nombre impair nombre impair + nombre impair = nombre pair et que le and correspond à la multiplication, puisque nombre pair * nombre pair = nombre pair nombre impair * nombre pair = nombre pair nombre pair * nombre impair = nombre pair nombre impair * nombre impair = nombre impair Xor (et and) sont donc associatifs et commutatifs (puisque l'addition et la multiplication le sont), l'élément neutre de xor est 0, et l'élément neutre de and est 1. On remarque aussi que la soustraction correspond au xor également: nombre pair - nombre pair = nombre pair nombre impair - nombre pair = nombre impair nombre pair - nombre impair = nombre impair nombre impair - nombre impair = nombre pair Xor est donc à la fois une addition et une soustraction, ce qui explique ton équation de tout à l'heure: plaintext + key = ciphertext -> plaintext = ciphertext - key, en remplaçant + et - par ⊕. On peut aussi en déduire l'identité suivante, un peu useless mais bon (ou le . dénote un AND): a . (b ⊕ c) = (a . b) ⊕ (a . c) |
|
|
|
|
« Sujet précédent | Sujet suivant »
|
Utilisateur(s) parcourant ce sujet : 1 visiteur(s)


 Accueil du forum
Accueil du forum Tableau de bord
Tableau de bord Liste des membres
Liste des membres Qui est en ligne?
Qui est en ligne? Mon profil
Mon profil Messages privés
Messages privés Nouveau message
Nouveau message Recherche
Recherche Calendrier
Calendrier Zine
Zine URL de redirection
URL de redirection Créer un PasteBin
Créer un PasteBin Classement (Top 100)
Classement (Top 100) Proposez un challenge!
Proposez un challenge!  Hacking
Hacking Hacking
Hacking  Spirit of hack
Spirit of hack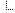 Messages: 32 816
Messages: 32 816 Client IRC en ligne
Client IRC en ligne

